Neste post iremos discutir as noções básicas de jogos de azar, e entender as probabilidades sobre os mais antigos e comuns que existem: a moeda e o dado.
O que são jogos de azar?
Jogos de azar são quaisquer tipos de jogos que baseiam o ato de vencer apenas na sorte de seus participantes. Ou seja, qualquer jogo em que, a chance de se vencer ou perder é definida apenas pelo acaso (ou sorte) dos jogadores, e a habilidade dos mesmos não aumentam as chances de vitória, é um jogo de azar.
Alguns dos exemplos mais conhecidos envolvem jogos com cartas (Poker, BlackJack, Truco, Cacheta etc.). Mas as cartas para esses jogos foram inventadas apenas no século IX na China e introduzidas na Europa apenas no século XIV. Neste post iremos focar nos jogos de azar mais antigos de que se tem registro: os dados e as moedas.
Uma breve história dos dados e da moeda:
Os primeiros dados da qual se tem registro foram descobertos em 1920, na região da Antiga Suméria e datam cerca de 2600 a.C. Eles possuiam formato de pirâmide e faces numeradas de 1 a 4, e presume-se que eram usados em jogos de adivinhação e para fins religiosos.
Alguns séculos mais tarde, os Assírios passaram a utilizar um osso extraído dos calcanhares de animais, denominado Astrágalo (ou Tálus), que era moldado até adquirir um formato de cubo, semelhante aos modelos mais atuais de dados de 6 faces.
Os jogos de azar foram criados pelos romanos por volta do século VII a.C., a partir da expansão do Império e da necessidade de distrair os soldados durante as campanhas de conquista por toda a Europa. Relatos escritos mostram que os soldados utilizavam dados rudimentares feitos similarmente aos Astrágalos para apostar suas rações diárias até as suas próprias vidas, como relatado por Tácito:
“Eles praticam o jogo de dados, em que um irá, naturalmente, se maravilhar, sobriamente, e bastante, como se fosse um negócio sério, com ousadia em ganhar e perder em que, quando eles não têm nada mais a jogar, eles apostam a sua liberdade e sua pessoa na última queda do dado. O perdedor resigna-se voluntariamente à servidão, e mesmo se ele é mais jovem e mais forte do que seu adversário, ele se permite ser amarrado e vendido. Assim, grande é a sua firmeza em um caso tão ruim: eles mesmos chamam isso de”manter a sua palavra“.”
O uso de moedas como meio de aposta foi criado também pelos romanos, durante os séculos V-III a.C., pois foi a partir deste momento que as tropas passaram a receber seus salários com moedas de prata, ao invés de sal. O jogo (na época chamado de navia aut caput (cara ou navio, em tradução livre)) consistia em se atirar uma moeda para cima e apostar na face que se acredita que irá cair virada para cima (muito similarmente aos jogos de cara ou coroa dos dias de hoje).
Os problemas desses jogos de azar da Antiguidade é que boa parte deles não era realmente aleatória, já que não havia meios de criar dados e moedas totalmente balanceados, levando a todos os tipos de trapaças com dados viciados e moedas desbalanceadas.
A probabilidade por trás dos dados e moedas
Vamos agora entender como funcionam as probabilidades que envolvem os principais jogos de azar com dados e moedas. Para fins de esclarecimento, todos os dados e moedas que serão utilizados nos exemplos são justos e balanceados, sem nenhum tipo de viés. Isso é um condição necessária para se analizar a aleatoriedade por trás deles, e não ocorrer nenhum problema causado por processos pseudoaleatórios (para mais informações sobre pseudoaleatoriedade, vide Pseudoaleatoriedade)
Analisando lançamentos de um dado honesto
Considerando um dado honesto (ou seja, um em que todas as faces possuem a mesma chance de ocorrência), vamos analizar como se comportam as probabilidades de sair o número indicado na face superior. Inicialmente, iremos focar em apenas um lançamento de um dado cúbico de 6 faces. Posteriormente iremos tratar de múltiplos lançamentos e de dados com mais ou menos faces. Mas antes, vamos nos lembrar de alguns conceitos básicos de probabilidade antes de começar:
Espaço amostral:
Suponhamos que um experimento (neste caso um lançamento um dado honesto) seja realizado sob certas condições fixas. Define-se o espaço amostral desse experimento como o conjunto de todos os resultados possíveis e denota-se por \(\Omega\).
No caso do lançamento de um dado de seis faces, o nosso espaço amostral é \(\Omega = \{ 1,2,3,4,5,6 \}\), pois esses são os únicos resultados possíveis.
Evento:
Um evento A é um subconjunto do espaço amostral, com \(A\subset\Omega\). Se atribuirmos um valor de probabilidade a esse evento, ele será dito aleatório. Analogamente, no lançamento de um dado de seis faces, os possíveis eventos são:
- \(A_1=\{1\}\);
- \(A_2=\{2\}\);
- \(A_3=\{3\}\);
- \(A_4=\{4\}\);
- \(A_5=\{5\}\);
- \(A_6=\{6\}\).
Vale ressaltar que os eventos, neste caso, são equiprováveis, ou seja, todos os eventos possuem a mesma chance de ocorrer, já que o dado é honesto.
Definição clássica de Probabilidade:
Seja \(\Omega\) um espaço amostral finito e A um evento, com \(A\subset\Omega\). A probabilidade de ocorrência do evento A é dada por: \(P(A)=\frac{A}{\Omega}\). Deste modo, podemos calcular a chance de ocorrer um resultado favorável no lançamento de um dado de seis faces.
Digamos que você esteja apostando com o seu amigo qual face irá cair virada para cima no lançamento de um dado. Você acha que será o número 5, enquanto o seu amigo acredita que será o número 2. A chance de ocorrer o evento \(A=\{5\}\) é de \(\frac{1}{6}\), já que há apenas um resultado em que o dado cairá com o número 5 com a face para cima. Similarmente, seu amigo possui a mesma chance de ganhar (\(\frac{1}{6}\)), pois o dado é honesto, e há apenas um resultado em que ele cairá com o número 2 com a face para cima.
Lançando um dado mais de uma vez:
Agora, considere que você e seu amigo estão lançando o dado duas vezes e estão apostando qual o valor da soma dos dois lançamentos. Como escolher em qual número apostar?
Vamos começar analisando o nosso espaço amostral. Como agora estamos lançando o dado duas vezes, vejamos quais são os possíveis resultados:
\(\Omega=\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),\)
\((2,1),(2,2),(2,3),(2,4),(2,5),(2,6),\)
\((3,1),(3,2),(3,3),(3,4),(3,5),(3,6),\)
\((4,1),(4,2),(4,3),(4,4),(4,5),(4,6),\)
\((5,1),(5,2),(5,3),(5,4),(5,5),(5,6),\)
\((6,1),(6,2),(6,3),(6,4),(6,5),(6,6)\}\).
Com isso, percebemos que o nosso espaço amostral agora possui 36 possíveis resultados. Vamos agora somar todos os valores do primeiro com o segundo lançamento de todos os eventos possíveis, e criar um segundo espaço amostral, desta vez com as somas como resultados:
\(\Omega=\{2,3,4,5,6,7,\)
\(3,4,5,6,7,8,\)
\(4,5,6,7,8,9,\)
\(5,6,7,8,9,10,\)
\(6,7,8,9,10,11,\)
\(7,8,9,10,11,12\}\)
Agora que possuímos todos os valores das somas de todos os possíveis resultados, vamos analisar quais as chances de cada número ganhar:
#Vamos primeiro criar um vetor com todas as possíveis somas:
soma<-c(2,3,4,5,6,7,3,4,5,6,7,8,4,5,6,7,8,9,5,6,7,8,9,10,6,7,8,9,10,11,7,8,9,10,11,12)
#Para facilitar a visualização, vamos organizar esses valores:
soma<-sort(soma)
soma
## [1] 2 3 3 4 4 4 5 5 5 5 6 6 6 6 6 7 7 7 7 7 7 8 8 8 8
## [26] 8 9 9 9 9 10 10 10 11 11 12
#Para descobrirmos o valor mais repetido, vamos encontrar a moda deste espaço amostral (Como o R não apresenta uma função de moda de maneira nativa, tive que criar a função para poder calcular):
getmode <- function(v) {
uniqv <- unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
moda<-getmode(soma)
moda
## [1] 7
#Agora, vamos criar um gráfico de barras para analizar a frequência de cada valor somado:
tab<-table(soma)
barplot(tab,col="blue",xlab = "Valor da soma",ylab="Frequência")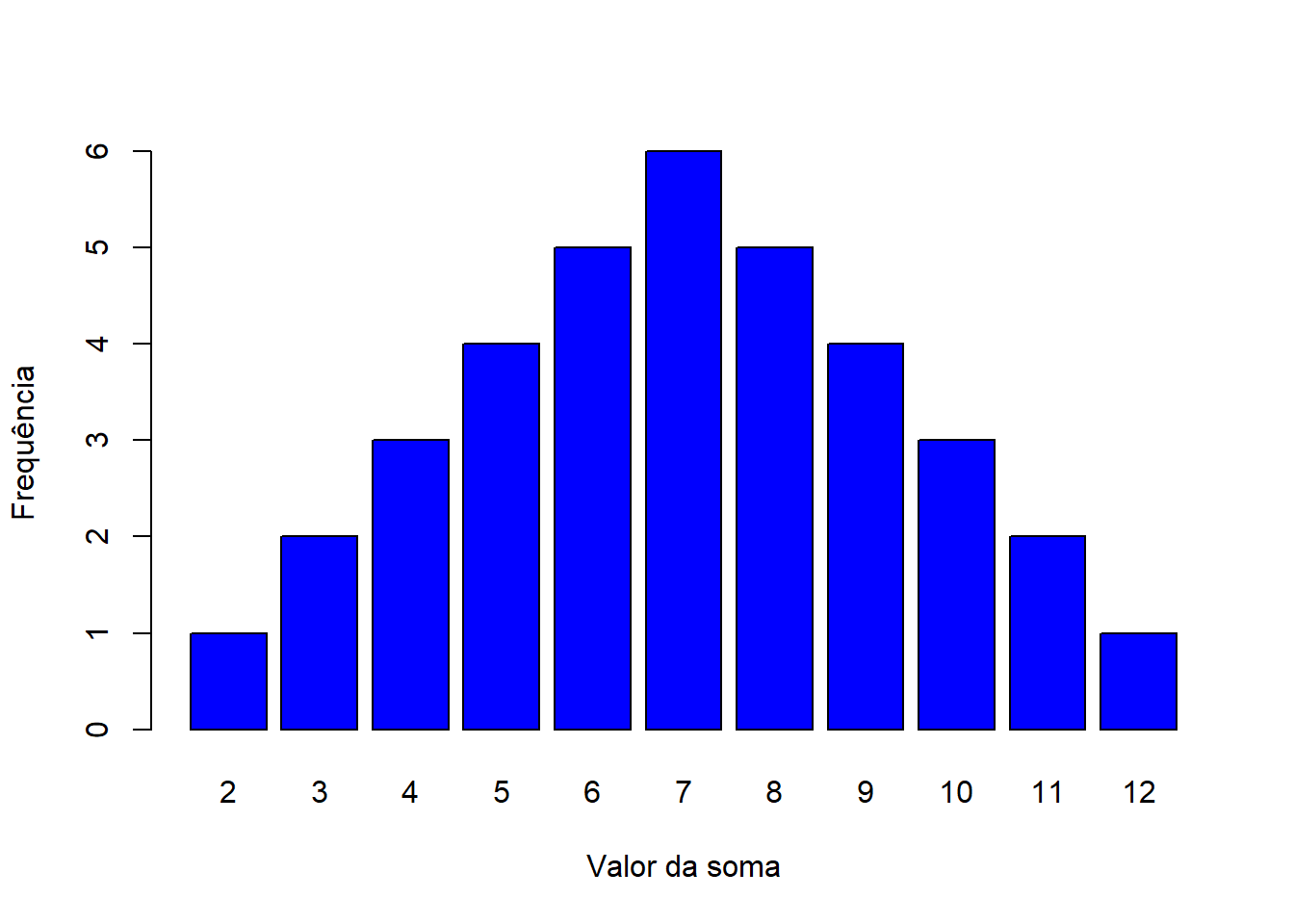
Como se pôde ver com auxílio do gráfico, o número 7 é o valor que mais se repete no espaço amostral, com 6 repetições em 36 possíveis resultados. Outros valores, como o 5 (que possui apenas 5 repetições) ou o 3 (que possui 3 repetições) são menos prováveis de se obter do que o 7. Com isso, agora você já sabe em qual valor apostar para ter mais chances de ganhar o jogo contra o seu amigo.
Probabilidade condicional com os dados:
Sejam dois eventos A e B subconjuntos do espaço amostral \(\Omega\), tais que \(A\subset\Omega\) e \(B\subset\Omega\). A probabilidade da interseção dos dois eventos (a chance de ocorrência de ambos os eventos) é dada por: \(P(A\cap B)=P(A)*P(B)\). Vale ressaltar que isso sóé possível se os eventos A e B forem independentes (o resultado do lançamento de um dado não interfere no resultado do seguinte, o que mostra que o lançamento de um dado duas vezes é um evento independente).
Por exemplo, em um dado honesto de 6 faces, qual a probabilidade de o resultado de um lançamento ser um número par e menor do que 5?
A partir da fórmula, podemos calcular essa probabilidade. Já sabemos o espaço amostral \(\Omega\), logo, vamos definir os eventos separadamente. Seja o evento A a ocorrência de valor par. Com isso, temos que \(A=\{2,4,6\}\) e que \(P(A)=\frac{3}{6}=\frac{1}{2}\). Agora, seja o evento B a ocorrência de número menor que 5. Com isso, temos que \(B=\{1,2,3,4\}\) e que \(P(B)=\frac{4}{6}=\frac{2}{3}\).
Como já sabemos a chance de se ocorrerem, separadamente, os eventos A e B, vamos calcular as chances de ocorrer ambos:
\(P(A\cap B)=P(A)*P(B)=\frac{1}{2}*\frac{2}{3}=\frac{2}{6}=\frac{1}{3}\)
Logo, a chance de o resultado de um lançamento de um dado ser par e menor que 5 é \(\frac{1}{3}\). Mas e se nós já soubéssemos de antemão que o resultado era menor que 5, qual seria a chance de o resultado ser par?
Chamamos esse caso de probabilidade condicional, pois já sabemos que ocorreu um evento, e ele se torna nosso novo espaço amostral. Para se calcular o valor de \(P(A\vert B)\) (lê-se probabilidade de A, dado B), usamos a fórmula: \(P(A\vert B)=\frac{P(A\cap B)}{P(B)}\).
No caso apresentado,já sabemos que o número é menor do que 5, e a probabilidade disso ocorrer é \(\frac{2}{3}\). Com isso, o nosso espaço amostral, que era \(\Omega=\{1,2,3,4,5,6\}\) agora é \(\Omega_B=\{1,2,3,4\}\). O valor \(P(A)=\frac{1}{2}\) não se alterou, já que ele mostra a chance de um número ser par, baseado no espaço amostral original. Agora, calculando a chance de ocorrer A, sendo que B já ocorreu, temos:
\(P(A\vert B)=\frac{P(A\cap B)}{P(B)}=\frac{\frac{1}{3}}{\frac{2}{3}}=\frac{1}{3}*\frac{3}{2}=\frac{3}{6}=\frac{1}{2}\)
Dados não-cúbicos:
Os dados mais comuns que existem são os que possuem formato de cubo, com 6 faces. Mas existem outros tipos de dados que não possuem essa forma.
Um dado que está cada vez mais ganhando espaço no mercado é o icosaedro, formado por 20 lados triângulares, devido ao seu uso em sessões de RPG ao redor do mundo. Ele oferece um espaço amostral muito maior do que os dados comvencionais, o que aumenta as possibilidades de uso.
Os outros dados que podem ser utilizados são os de 4,8 e 12 lados (tetraedro, octaedro e dodecaedro). Mas por que não fazer com qualquer número de lados, por exemplo 100?
Isso se deve ao fato de que esses sólidos (tetraedro, cubo, octaedro, dodecaedro e icosaedro) são os únicos sólidos platônicos, que são completamente honestos devido à sua simetria. Quaisquer outro sólido não será balanceado, e possuirá viés em seus lançamentos.
E como se comportam as probabilidades desses dados não-cúbicos? Simples: como sabemos que todos eles são balanceados e que, para cada lançamento, todas as faces possuem a mesma chance de caírem voltadas para cima, a chance de um certo número escolhido ser o vencedor é de \(\frac{1}{n}\), com \(n=\) número de faces do dado.
Por exemplo, a chance de um dado em formato de icosaedro (d20, para os mais íntimos) cair com o número 20 virado para cima é de \(\frac{1}{20}\). Vale ressaltar que todas as propriedades de cálculo de probabilidades (Interseção de eventos, probabilidade condicional etc) também se aplicam a dados não-cúbicos.
E as moedas?
As moedas são primordialmente mais fáceis de se analizar. Para cada lançamento, há apenas dois possíveis resultados: Cara ou Coroa. Logo, a probabilidade de se cair um resultado esperado é de \(\frac{1}{2}\), e se diversos lançamentos forem realizados, a chance de n jogadas serem favoráveis é de \((\frac{1}{2})^n\). De onde surgiu esse resultado?
Vamos voltar à probabilidade de interseção de eventos. Digamos que você quer lançar a moeda 5 vezes, e anotar o resultado da face superior. Qual a chance de todos os lançamentos resultarem em Cara? O nosso espaço amostral é \(\Omega=\{(c,c,c,c,c),(c,c,c,c,k),(c,c,c,k,c),...,(k,k,k,k,c),(k,k,k,k,k)\}\) (note que o número de resultados possíveis é 32, já que podemos calcular o tamanho de \(\Omega\) por meio de permutações. Temos 5 lançamentos, cada um podendo adotar um de dois valores (Cara ou Coroa), logo temos \(2^5 = 32\) possíveis resultados de lançamentos).
Portanto, a chance de se ocorrerem 5 lançamentos seguidos que resultem em Cara é de \(\frac{1}{32}\).
Bônus: Gerador de lançamentos de dados e moedas em R:
Agora que já sabemos como funcionam as probabilidades por trás de lançamentos de moedas e dados, vamos criar um gerador de lançamentos pelo R. Comecemos com o básico:
#Vamos começar com as moedas. Criaremos um vetor com os possíveis resultados:
moeda<-c("Cara","Coroa")
#Agora, vamos utilizar a função sample para gerar uma amostra de lançamentos do tamanho que quisermos, como por exemplo, 10 lançamentos:
jogadas_moeda<-sample(moeda,size = 10,replace = TRUE,prob = NULL)
jogadas_moeda
## [1] "Coroa" "Coroa" "Coroa" "Coroa" "Coroa" "Coroa" "Cara" "Coroa" "Coroa"
## [10] "Coroa"
#Para amalizarmos se essa moeda é honesta teremos que aumentar o número de lançamentos. Assim, poderemos ver a razão entre o número de Caras e de Coroas:
jogadas_moeda<-sample(moeda,size=1000,replace = TRUE,prob = NULL)
#Agora que temos uma amostra com 1000 lançamentos, vamos ver quantas Caras e quantas Coroas saíram (não irei mostrar o total de lançamentos para poupar espaço na tela):
numero_caras<-length(jogadas_moeda[jogadas_moeda=="Cara"])
numero_coroas<-length(jogadas_moeda[jogadas_moeda=="Coroa"])
numero_caras
## [1] 502
numero_coroas
## [1] 498
prob_cara<-numero_caras/1000
prob_cara
## [1] 0.502
prob_coroa<-numero_coroas/1000
prob_coroa
## [1] 0.498
#Note que esses valores se concentram próximos de 0,5 , que é a probabilidade de se cair cara ou coroa com um lançamento de uma moeda honesta. Podemos então afirmar que esse gerador de lançamentos é honesto.
#Agora vamos para os dados. Vamos começar com um dado de 6 faces numeradas de 1 a 6:
dado<-c(1,2,3,4,5,6)
#Como fizemos com a moeda, usamos a função sample para gerar uma amostra de n lançamentos independentes. Comecemos com 10:
jogadas_dado<-sample(dado,size =10,replace = TRUE,prob=NULL )
jogadas_dado
## [1] 2 5 6 4 6 5 6 3 6 2
#Para analizarmos as probabilidades desse dado, vamos aumentar o número de lançamentos:
jogadas_dado<-sample(dado,size=1200,replace = TRUE,prob=NULL)
#Agora vamos organizar esses lançamentos para que fique mais fácil de se observar:
jogadas_dado<-sort(jogadas_dado)
#Para aqueles que forem mais curiosos e quiserem criar um gáfico com os lançamentos:
plot(jogadas_dado,main="Lançamentos de dado",xlab = "Número de lançamentos",ylab = "Valor do dado")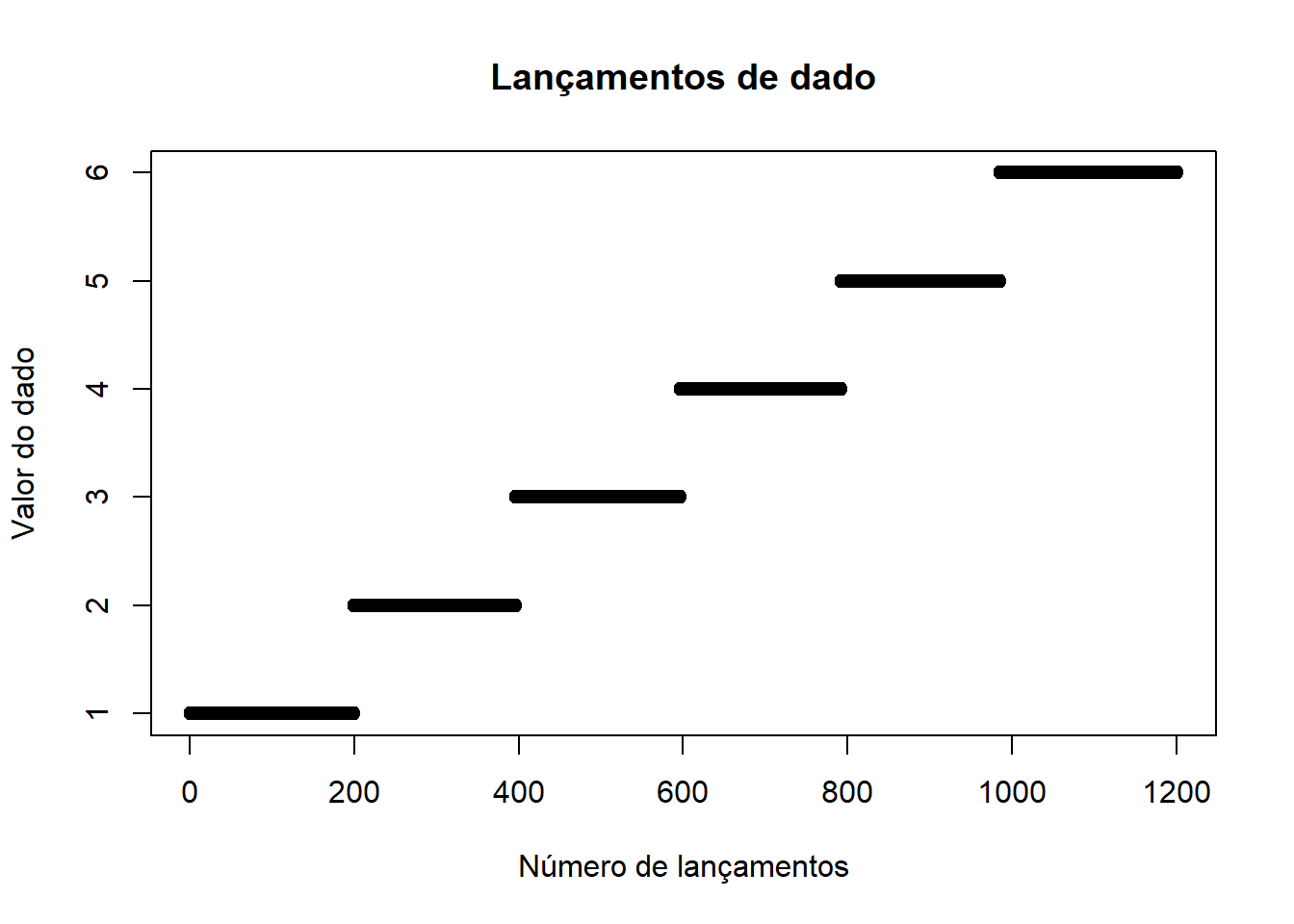
#Com a análise dos gráficos pôde-se perceber que os lançamentos foram aproximadamente bem divididos por todos os 6 valores possíveis do dado. Ainda assim, vamos confirmar os valores exatos de cada número:
numero_1<-length(jogadas_dado[jogadas_dado==1])
numero_2<-length(jogadas_dado[jogadas_dado==2])
numero_3<-length(jogadas_dado[jogadas_dado==3])
numero_4<-length(jogadas_dado[jogadas_dado==4])
numero_5<-length(jogadas_dado[jogadas_dado==5])
numero_6<-length(jogadas_dado[jogadas_dado==6])
numero_1
## [1] 199
numero_2
## [1] 197
numero_3
## [1] 200
numero_4
## [1] 196
numero_5
## [1] 193
numero_6
## [1] 215
#Percebemos então que os valores que representam quantas vezes cada número apareceu está em torno de 200 lançamentos por número. Vamos calcular, baseado nos números obtidos, a probabilidade de cada um:
prob_1=numero_1/1200
prob_2=numero_2/1200
prob_3=numero_3/1200
prob_4=numero_4/1200
prob_5=numero_5/1200
prob_6=numero_6/1200
prob_1
## [1] 0.1658333
prob_2
## [1] 0.1641667
prob_3
## [1] 0.1666667
prob_4
## [1] 0.1633333
prob_5
## [1] 0.1608333
prob_6
## [1] 0.1791667
#Com isso, confirmamos que as probabilidades de cada número sair ganhador é de aproximadamente 1/6, mostrando que o dado é honesto. Se quisermos criar dados de mais lados, é só aumentar o vetor que contém os valores. Por exemplo:
d_4<-sample(c(1:4),size=1,replace = TRUE,prob = NULL)
d_8<-sample(c(1:8),size=1,replace = TRUE,prob = NULL)
d_12<-sample(c(1:12),size=1,replace = TRUE,prob = NULL)
d_20<-sample(c(1:20),size=1,replace = TRUE,prob = NULL)
d_4
## [1] 4
d_8
## [1] 3
d_12
## [1] 11
d_20
## [1] 9
